不老不死への科学

無限時間における確率淘汰

【概論】
抗老化技術、再生医療、ナノマシンによる細胞修復技術により人間の体を半永久的に維持できるようになったとしよう。
だがそれだけでは人間は永遠の命を手にしたとは言えない。
実際、不老不死の技術が完成したとしても、人口問題(人口過剰による空間や資源の枯渇)、環境問題、戦争の勃発、太陽系の消滅、宇宙の崩壊など様々な課題が残る。
また、人間は何らかの事故によっても死ぬことがある。
自動車・電車・航空機などの交通機関での事故や、自然災害による事故など様々な原因によって死ぬ可能性があるのである。
これを「確率的に淘汰(選択)される」と言うことにしよう。
これは１００年程度の期間では、ほとんど無視できるほどに影響力は小さい。
だが、無限の時間の中では絶大な影響力を持って、生命を奪う要因となるのである。
果たして人類はこの問題にどのように対処していけば良いのか？
そもそも科学技術により克服できる問題なのか？
このような課題を踏まえた上で、これから確率淘汰という現象について考察していくことにする。

【事故死の確率】
統計データによると、１９９８年に事故死した男性（１〜２９歳）は約５０００人（約２３１１万人中）、女性（１〜２９歳）は約１０００人（約２４０３万人中）である。
つまり一年間で若い人が事故に遭う確率(一年間で事故死した人数/総人口)は
男性の場合０．０２１６４％
女性の場合０．００４１６％
と計算できる。
では実際に不老不死の時代になり、若い状態でかなり長い時間を生きられるようになったら、事故により死んでしまう確率はどのくらいなのか？
実際にプログラムを組んで計算した。
ただし、毎年一人の人が事故に遭う確率は一定であると仮定する（つまり、安全性の向上による事故死の確率の低下による影響を無視する）。
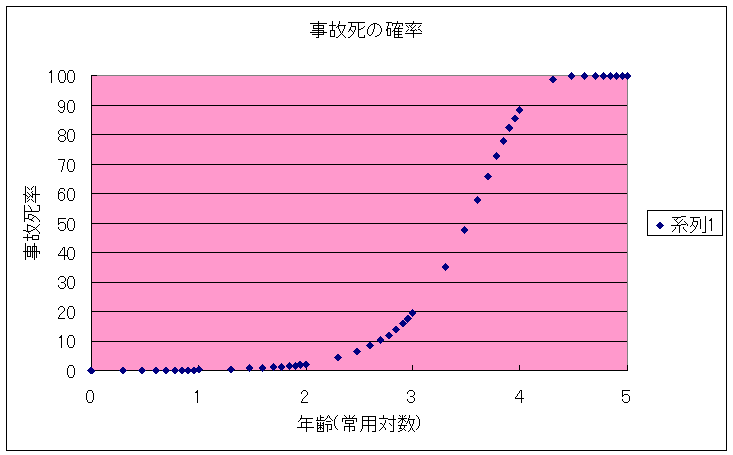
男性の場合の結果をグラフにプロットすると以下のようになる。

横軸は年齢の常用対数をとったもので、縦軸は事故死する確率である。
常用対数とは数値にlog10という関数をかけたもので、その数が１０の何乗かを表したものである。

グラフを見ると１０００年の間に約２０％が事故死し、そこから急激に死亡率が増加し１００００年の間には９０％近い人が死ぬことになる。
また１０００００万年もするとほぼ１００％の人が死亡する。
つまり、事故に対する安全性の向上がない場合、不老不死になったとしても、ほぼ確実に確率的に淘汰されると言える。
これに対処する方法は、科学技術の進歩により社会的な事故に対する安全性を高めていくことである。
つまり、電車が脱線して建物に突っ込んだとしても、電車が衝撃を吸収し、中の乗客には被害が及ばないような仕組みになっていれば、かなり安全であると言えるし、また自然災害を予め予測したり、建物の強度を高めたりすることでも安全性を高めることができる。例え、運悪く事故に遭ってしまったとしても、医療技術が発達していれば多くの人を救うことができる。

ではどのくらいの速さで安全性を向上していけば良いのか？
おそらく事故死率を完全に０にすることはできないかもしれないが、事故死率をある一定の法則に従って減らしていけば、生き残る可能性が出てくるのである。

事故死率を減らす速度を考えるには、まず、数学的にギリギリ事故死率が１００％になるという関数を考えて、それよりも速い速度で確率を減少させていけば良い。また、確率が０に近づくにつれて安全性の向上は難しくなる。つまり時間が経つにつれて事故死率の減少がだんだんゆるやかになっていかなければならない。

それでは、事故死率がギリギリ１００％になる場合を考える。
それはある一定期間が経過するごとに、事故死率を1/2倍、1/3倍、1/4倍、1/5倍・・・と減少させていくのである。
最初の段階では確率を1倍から1/2倍に下げる必要があるが、10000年後には、確率を1/10000倍から1/10001倍にすれば良いだけなので、ほとんど安全性を向上させる必要はない。だが、10000年もすれば安全性もかなり向上し、事故死率も０にかなり近いているであろうから、確率の減少分は少ないほうが良い。
１０００年ごとに上のように確率が減少するとして、この場合の事故死率を計算し、プロットすると以下のようになる。

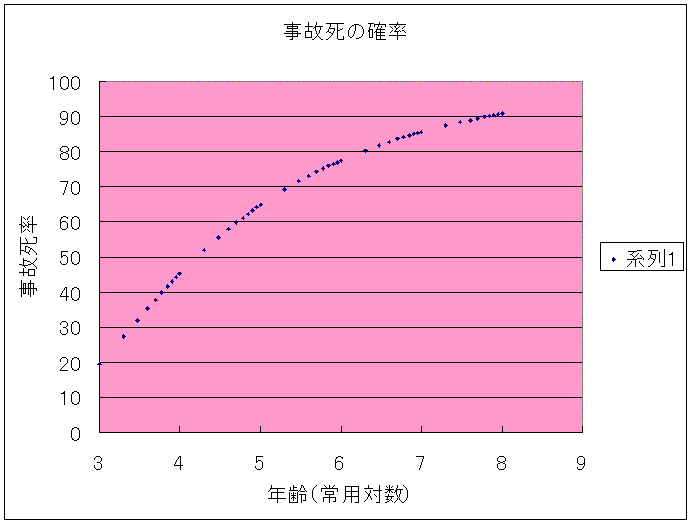
ゆるやかな曲線を描きながらだんだん確率が増加している。
一億年経過した場合、９０％の人が死んでしまう。
かなり事故死の影響を緩めることができるが、それでも１億年もすればかなりの人が死亡し、ゆっくりと確率は１００％に近づいていく。

では、これ以上の速度で安全性を向上させたらどうか？
一例として、１０００年が経過するごとに、事故死率を1/4倍、1/9倍、1/16倍、1/25倍・・・と減少させていく。
この場合も最初の確率の減少分は大きいが、だんだんゆるやかに減少していく。
この場合の計算結果をプロットすると以下のようになる。

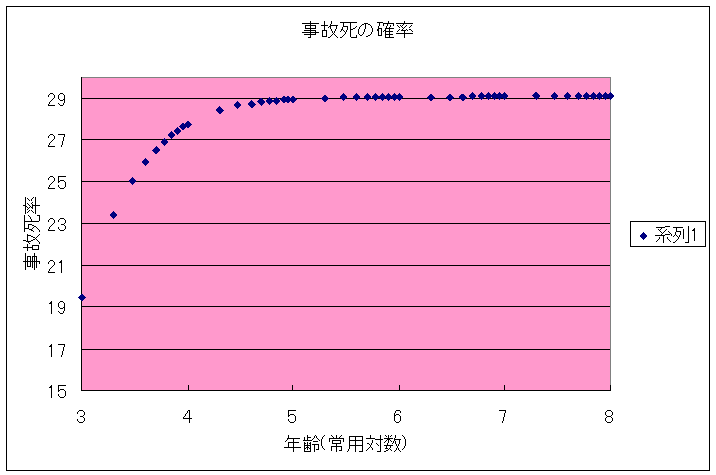
このグラフは今までのグラフとは明らかに違う。
１０００００万年まで事故死率は増加し、約２９％の人が死亡するが、それ以降の死亡率の増加がほとんどなく、１億年経過しても、死亡率は約２９％であり、７１％の人は確率により淘汰されないのである。

【結論】
以上の考察から、科学技術の進歩により確率による淘汰から免れることは可能である。
だが、それには永遠に研究を続け安全性を向上していく必要がある。
仮にどこかで科学の進歩が止まり、事故死率が一定値を取れば、必ず死亡率は１００％に近づいていく。
不老不死の実現は終わることのない戦いであると言うことができるのである。

最も、人類が上で述べたように努力を続けたとしても、２９％の人は死を免れることはできない。
これは確率的な人類の選別であり、人間が意図的に操作できない要素である。
２１％の人は永遠の無へと消えていき、７１％の人は永遠の可能性を手にする。
確かにこれは不公平で、理不尽な現象であるが、これが残酷な現実であると受け止めるしかない。

では、どうすれば生き残ることができるのか？
誰が生き残るのか？
生き残るための対処策は、常に事故の危険がある場所に行くのを避けたり、非常事態に備えて生き残る訓練を行うくらいしかない。自己を守る能力を磨き、常に生き残る方法を考えていく必要があるかもしれない。
何が何でも生きたいという強い意志を持つことが、生き残るための最善の策であると言える。

それでも、人類は確率的に無条件に選別されるため、誰が生き残るかは実際にその時になってみないと分からない。
ストーリーの結末としては、いわゆる善人が生き残り、悪人が死ぬというのが、大衆受けするのかもしれない。
だが、おそらくは、善人も悪人も関係なく、ランダムに選ばれた者が死んでいくというのが現実である。